

If you use one of these packages, you don’t need the above equation.
Fft windowing software#
Some commercial DSP software packages merely require that you specify Atten Cheb in decibels rather than specify g. If you needed side-lobe levels to be no greater than –60 dB below the main lobe, you’d use the above equation to establish a g value of 3.0 and let your FFT software generate the Chebyshev window coefficients. The Chebyshev window function’s stop-band attenuation, in decibels, is equal to
Fft windowing windows#
Figure 1a shows the windows that result for three values of g, and Figure 1b shows the corresponding frequency responses for each window. The graphs in Figure 1 show how different g values can affect the window and the frequency response for a Chebyshev window function. You only need to realize that the “control” parameters g and b let you adjust the windows’ main-lobe widths versus their side-lobe levels. In fact, most commercial digital-signal-processing (DSP) software packages have built-in functions that evaluate w(n) Cheb and w(n) Kaiser. Don’t let the complexity of these equations intimidate you-at this point, you need not be concerned with their mathematical details. In both expressions, N represents the number of time-domain points in the window functions. Two formidable-looking expressions define their time-domain samples ( Eq. The two window functions that provide such flexibility go by the names Chebyshev (or Dolph-Chebyshev) window function and Kaiser (or Kaiser-Bessel) window function. Now you will find out how two popular window functions let you strike a compromise between widening a window’s main lobe and reducing its side-lobe levels.
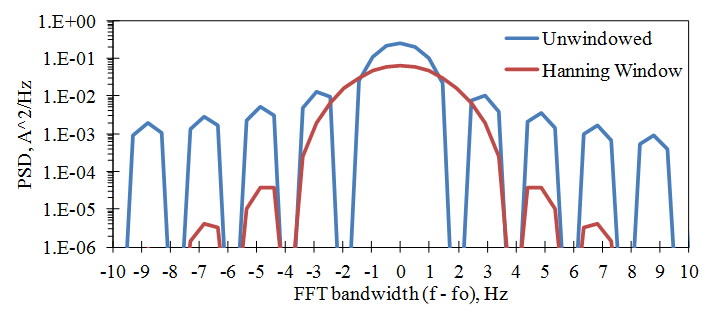
Their amounts of leakage (side-lobe level reduction) and resultant loss in frequency resolution (main-lobe widening) are fixed. The window functions discussed in Part I (Hamming, Hanning, Blackman-Harris, and rectangular) have a limitation. But that reduction comes at the expense of degraded frequency resolution. The article explained how a simple window function applied to time-domain data reduces inherent FFT spectral leakage distortion. In the first article, I explained how you can use window functions to minimize that frequency-domain distortion when you’re performing spectral testing.
Fft windowing series#
The first article in this two-part series (Footnote 1) explained the cause and spectral smearing effect of “leakage” in the fast Fourier transform (FFT).


 0 kommentar(er)
0 kommentar(er)
